Day 7 of AoC 2020 (Handy Haversacks) is when the problems get a little bit harder to solve. However, it is a good example to use a directed acyclic graph (DAG) to visualize and solve the problem. Spoilers ahead.

Let’s start off with the example given in the problem.

light red bags contain 1 bright white bag, 2 muted yellow bags.
dark orange bags contain 3 bright white bags, 4 muted yellow bags.
bright white bags contain 1 shiny gold bag.
muted yellow bags contain 2 shiny gold bags, 9 faded blue bags.
shiny gold bags contain 1 dark olive bag, 2 vibrant plum bags.
dark olive bags contain 3 faded blue bags, 4 dotted black bags.
vibrant plum bags contain 5 faded blue bags, 6 dotted black bags.
faded blue bags contain no other bags.
dotted black bags contain no other bags.

This looks like a good candidate for a graph. The above example can be visualized as shown in the diagram below.

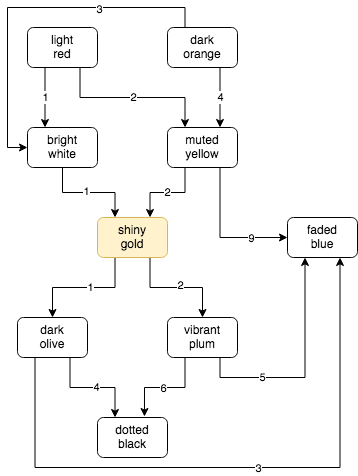
As you can see from the diagram, faded blue bags contain no other bags, but are contained within muted yellow, vibrant plum and dark olive bags. Also, no bags contain light red or dark orange bags.

Given the way the problem is presented, we can assume that the input does not have any cycles, and this is definitely true of the example. Also, the problem states that you have a shiny gold bag; which is highlighted in the diagram above.

Part 1 requires us to determine how many colored bags can eventually contain a shiny gold bag. If you see the diagram above, and follow the arrows in the reverse order from shiny gold, you will see that there are 4 colored bags which can eventually contain a shiny gold bag; bright white and muted yellow, which can contain the shiny gold bag directly, and light red and dark orange, which can contain bright white and muted yellow bags. A faded blue bag can be contained in 7 other colored bags, while a bright white bag can be contained in 2 other colors.

Now that we have an understanding of the problem, let’s get down to actually solving it. Our first task is to parse the input and generate a graph for our use. We can use the re module to match against the text and get the actual results we need. Also, the defaultdict is useful in making sure that we have a default empty list to start off with, and reduces the amount of code we need to type.

import re
from collections import defaultdict

contain_regex = re.compile(r'(.*) bags contain')
inner_regex = re.compile(r'(\d+) (.*?) bags?[,.]')

contains = collections.defaultdict(list)
contained_in = collections.defaultdict(list)

with open('input') as datafile:
    for line in datafile:
        # All lines will match contain_regex
        outer = contain_regex.match(line)[1]

        for m in inner_regex.findall(line):
            contains[outer].append((int(m[0]), m[1]))
            contained_in[m[1]].append(outer)

Now, we just need to recursively add the contained_in values to a set, starting with the key shiny gold. However, there is a possibility that this will recompute some values. If we take a naive approach to recursively calculate the container bags, we will repeat some calculations. With the example above, bright white and muted yellow bags are both contained in light red and dark orange bags, causing the computation for the latter to be repeated. This can be avoided by using memoization, and this is easily handled with functools.lru_cache. The cache size can be set to the size of the input, which will essentially guarantee that no calculations will be repeated.

@functools.lru_cache(maxsize=len(contained_in))
def count_bags(bag):
    ret = set()
    for b in contained_in[bag]:
        ret.add(b)
        ret.update(count_bags(b))

    return ret

part1 = count_bags('shiny gold')
print(len(part1))

For part 2, we need to recursively compute the number of bags that a shiny gold bag must contain. We can use the same pattern to use memoization to save partial results. With the example above, a shiny gold bag must contain:

• 1 dark olive bag, which in turn contains:
  • 3 faded blue bags
  • 4 dotted black bags
• 2 vibrant plum bags, each of which contain:
  • 5 faded blue bags
  • 6 dotted black bags

As you can see, the shiny gold bag must contain a total of 32 bags. This can be recursively computed with the code below.

@functools.lru_cache(maxsize=len(contained_in))
def bag_cost(bag):
    cost = 0
    for b in contains[bag]:
        cost += b[0] * (1 + bag_cost(b[1]))

    # Or as a one liner
    cost = sum(b[0] * (1 + bag_cost(b[1])) for b in contains[bag])

    return cost

part2 = bag_cost('shiny gold')
print(part2)